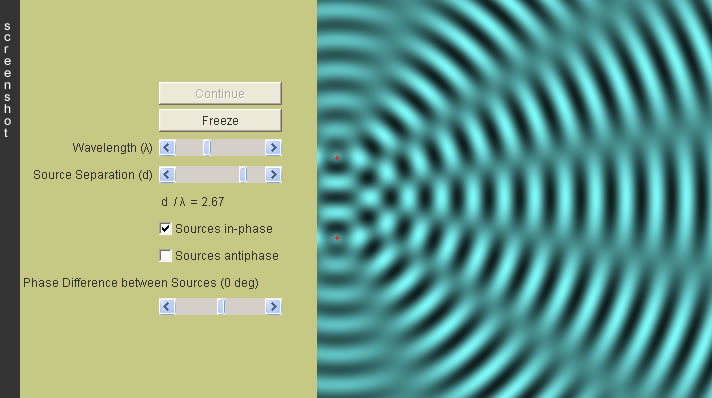
|
 |
Simply speaking,
the kind of interference taking place at a specific point,
say P, is determined by the phase
difference between the two sources (the two black dots),
and the phase difference arising from the two unequal paths
of travel of the two waves to that point.
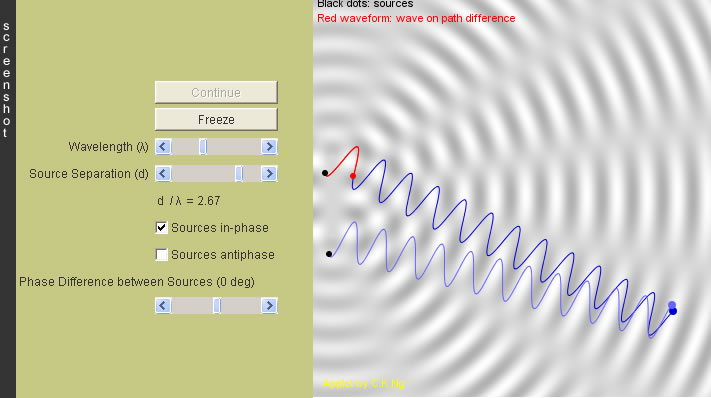
In the figure shown,the red waveform is the subtraction of the lower wave train from
the upper one. After taking that, the two remaining parts (colored in blue) becomes equal in length.
So, this red waveform is crucial and enough in knowing the phase difference of the second cause mentioned above.
Phase difference between the two waves arriving at P =
Phase difference between the two sources (the two black dots) + Phase difference
between the beginning and the end point of the red waveform
|
|
| (I) |
In particular, when the two sources are in-phase, then we only need
to consider the effect from the path difference, which varies with the observation point P. As we know,
wave repeats itself periodically over whole wavelengths.
If the path difference (the red waveform) contains,
e.g., 3 whole wavelengths, this means one of the two waves upon
arrival at P will be shifted by 3 wavelengths more than the
other; but importantly a shift of 3 wavelenths is equivalent
to "zero shift". Since the two waves are in-phase
as they are emanated, and such a path difference does not cause an additional nonzero phase shift, so they are still
in-phase when they arrive at P. Hence, as the two waves meet and are added together there,
a big up-down oscillation (constructive interference) is formed.
It is easy for us to conclude that:
|
| |
• If the red waveform contains an integral number of wavelengths, the two waves arriving
at P must be in-phase, i.e., |
| |
|
constructive interference occus at P when Path Difference =
0, λ, 2λ, 3λ, .... |
| |
• On the contrary, if the red waveform contains an integral number plus a half wavelength, the two waves
arriving at P must be in anti-phase, i.e., |
| |
|
destructive interference occurs at P when Path Difference
= 0.5λ, 1.5λ, 2.5λ,...., where λ is the wavelength. |
| |
|
|
| (II) |
If the two sources are in anti-phase, the two
waves are "exactly opposite" at the moment of leaving
their sources. |
| |
A shift of a half wavelength
because of the path difference will be just right to make them in-phase. |
| |
Therefore, the conditions now become |
| |
Constructive interference occurs at P when Path Difference
= 0.5λ, 1.5λ, 2.5λ,.. |
| |
Destructive interference occus at P when Path Difference =
0, λ, 2λ, 3λ, .... |
| |
|
| (III) |
If the two sources have a phase difference, say π/3, what will the conditions of interference become? |
| |
|
| Question: |
| |
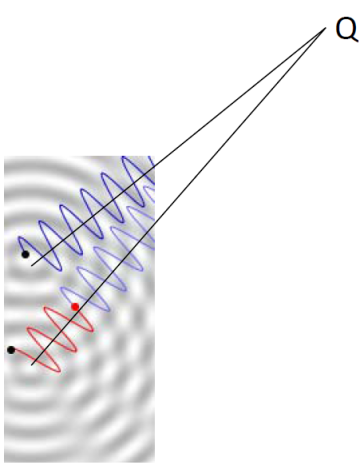
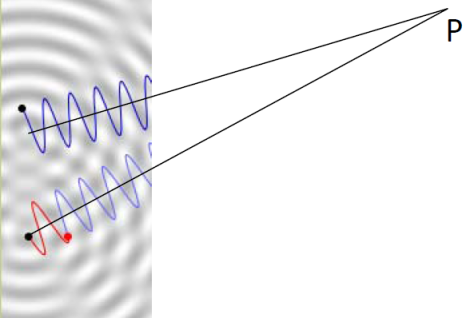 |
In the diagrams, P and Q are two points on the same interference pattern.
The two sources are not necessarily in-phase.
If the interference at P is destructive, what is the interference at Q ?
|
 |
|
|
|
|
|