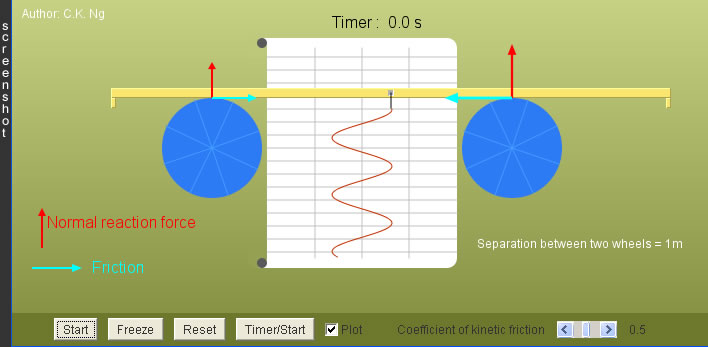
SHM Oscillator
1. Drag the beam to one side and then press "Start". Use the timer to record the time for, say, 20 complete cycles.
2. Repeat the above step, but with a larger or smaller amplitude. Is the period independent of amplitude ?
| ||||
| ||||
Question : | ||||
A common notion about shm is that kinetic energy is converted to potential energy, and vice versa as the oscillation continues; the sum of the kinetic and potential energy is a constant. In this example, there seems no involvement of any potential energy; where does the kinetic energy come from and go to ? |
|
Run outside of the browser by pressing 'Enter' or double-clicking the Jar file |
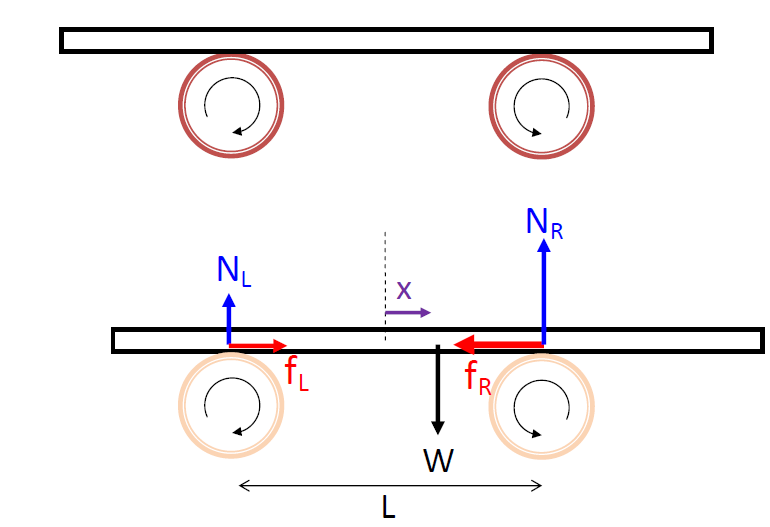 |
|
A uniform plank of mass m is supported horizontally and symmetrically by two identical rollers of fixed axes and of centers separated by a distance L.
The rollers rotate in the opposite directions, always pushing the plank back to the central position, as shown in the above diagrams. |